-
Armadillo employs a delayed evaluation approach to combine
several operations into one and reduce (or eliminate) the need for temporaries.
Where applicable, the order of operations is optimised.
Delayed evaluation and optimisation are achieved through recursive templates and template meta-programming.
-
While chained operations such as addition, subtraction and multiplication (matrix and element-wise) are the primary targets for speed-up opportunities,
other operations, such as manipulation of submatrices, can also be optimised.
Care was taken to maintain efficiency for both "small" and "big" matrices.
-
See also the Questions page for more information about speed enhancements.
-
Below is a set of timing comparisons against two other C++ matrix libraries
(IT++ and Newmat)
which have comparable functionality.
The comparisons were done using an Intel Core2 Duo CPU (2 GHz, 2 Mb cache), Linux kernel 2.6.26, GCC 4.3.0.
In each case the value of N
(see the code below) was empirically found so that each test took at least 5 seconds.
Code extract
// size and N are specified by the user on the command line
mat A = randu(size,size);
mat B = randu(size,size);
...
mat Z = zeros(size,size);
timer.tic();
for(int i=0; i<N; ++i)
{
Z = A+B; // or Z = A+B+C ... etc
}
cout << "time taken = " << timer.toc() / double(N) << endl;
Add two matrices
Z = A+B

Matrix size: 4x4
|
Approximate
speed-up relative to
IT++:
|
15
times |
Newmat:
|
10
times |
|
|

Matrix size: 100x100
|
Approximate
speed-up relative to
| IT++: |
3.5
times |
| Newmat: |
same
speed |
|
|
Add four matrices
Z = A+B+C+D

Matrix size: 4x4
|
Approximate
speed-up relative to
| IT++: |
15
times |
| Newmat: |
10
times |
|
|

Matrix size: 100x100
|
Approximate
speed-up relative to
| IT++: |
6
times |
| Newmat: |
1.5
times |
|
|
Multiply four matrices
Z = A*B*C*D
Here matrix A has more elements
than B, which in turn has more elements than C, and so on. In this case
it is more efficient to multiply the matrices "backwards", which is
automatically done by Armadillo.

A: 100x80
B: 80x60
C: 60x40
D: 40x20
|
Approximate
speed-up relative to:
IT++:
|
2.5
times
|
Newmat:
|
10
times
|
|
|

A: 1000x800
B: 800x600
C: 600x400
D: 400x200
|
Approximate
speed-up relative to:
| IT++: |
2.5
times
|
| Newmat: |
20
times
|
|
|
Submatrix manipulation
B.row(size-1) = A.row(0)
Copy first row of matrix A into last row of matrix B

Matrix size: 4x4
|
Approximate
speed-up relative to:
IT++:
|
16
times
|
Newmat:
|
44
times
|
|
|

Matrix size: 100x100
|
Approximate
speed-up relative to:
IT++:
|
2
times
|
Newmat:
|
4.5
times
|
|
|
Multi-operation expression
colvec p = randu(size);
colvec q = randu(size);
colvec r = randu(size);
...
double result = as_scalar(trans(p) * inv(diagmat(q)) * r);
The above is an example of a multi-operation expression that is detectable by Armadillo
(multiply the transpose of a column vector by the inverse of a diagonal matrix, then multiply by a column vector).
The above set of operations is compiled into a single loop, without creating any temporary matrices or vectors.

Matrix size: 4x4
|
Approximate
speed-up relative to:
IT++:
|
77 times
|
Newmat:
|
23 times
|
|
|
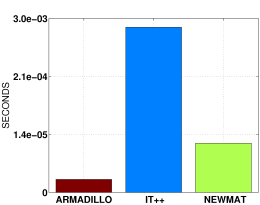
Matrix size: 100x100
(y-axis is non-linear)
|
Approximate
speed-up relative to:
IT++:
|
1086 times (!)
|
Newmat:
|
5 times
|
|
|